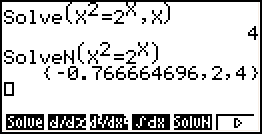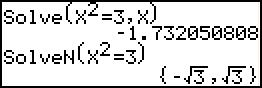Er zijn allerlei manieren om vergelijkingen te laten oplossen door je grafische rekenmachine.

• met ROOT (F1) nulpunten bepalen
  1. Met de pijltjes omhoog/omlaag en EXE kun je zonodig de goede grafiek kiezen
  2. De cursor gaat naar het (eerste) snpijpunt met x-as, en de coördinaten staan onder op het schermpje
  3. Met pijltjes links/rechts kun je eventuele andere nulpunten laten zoeken

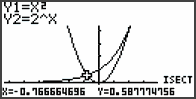
• met ISCT (F5) snijpunt(en) van twee grafieken bepalen.
  1. Met de pijltjes omhoog/omlaag en EXE kun je zonodig kiezen om welke twee grafieken het gaat
  2. De cursor gaat naar het (eerste) snpijpunt en de coördinaten zijn af te lezen
  3. Met pijltjes links/rechts kun je eventuele andere snijpunten laten zoeken
• X-CAL (F6 F2) De X bepalen bij een gegeven uitkomst (Y)
  1. Met de pijltjes omhoog/omlaag en EXE kun je zonodig de goede grafiek kiezen
  2. Typ de uitkomst (Y-waarde) in
  3. De cursor gaat naar het (eerste) punt , en de coördinaten worden getoond.
  4. Met pijltjes links/rechts kun je eventuele andere punten laten zoeken met de zelfde Y waarde

Er worden alleen oplossingen gezocht binnen de opgegeven x-waarden. De instellingen van het V-Window, met name X_min en X_max zijn dus van belang.

Coordinaten van het laatst berekende punt zijn in andere menu's op te roepen met X (ALPHA +)[(of X,θ,T ] en Y (ALPHA −)

We kiezen als vergelijking: x² = 6 − 4x

1. voorbereiding
   1. Herleid de vergelijking op nul: x² + 4x −6 = 0
   2. Kies uit het hoofdmenu EQUA (X,θ,T )
   3. Kies F2 (Polynomial)
   4. Kies F1 (2e graads)
2. (laten) oplossen
   
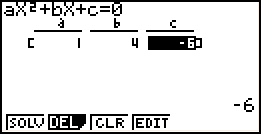
   1. Typ de juiste waarden in (bedenk dat a=1; b=4; c= - 6)
   1. 1 EXE 4 EXE -6 EXE
   2. Druk op F1 of op EXE
   2. Neem de bruikbare waarden over en rond ze eventueel verstandig af
   1. Linksboven staat als antwoorden 1.1622 en -5.162 deze zijn afgekapt, dus vaak niet juist afgerond
   2. Je kunt met de cursortoets een van beide antwoorden selecteren
   3. Rechts onderaan staat het exacte antwoord (of een een benadering)
   4. Je kunt (vaak) met F↔D wisselen tussen exacte en benaderde waarden
   5. Ga na of je alle oplossingen kunt/moet gebruiken, en of een exact antwoord of een benadering beter is.
      Als je antwoorden met i krijgt wordt er gerekend met complexe getallen. Dit is aan te passen via SET UP (SHIFT MENU)
      
   
3. achteraf
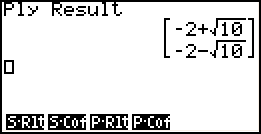
   • Je kunt later de oplossingen in een ander menu (bijv. menu 1: RUN-MAT) oproepen via VARS: F6 F3 (EQUA) F3 (P-Rlt)

Het oplossen van vergelijkingen met EQUA Solver is erg populair, maar heeft een paar nadelen:

• Je krijgt in eerste instantie één oplossing
• De uitkomst wordt beïnvloed door toevallige factoren, zoals de waarde van X op dat moment

Dit menu is vooral handig wanneer bij vergelijkingen met meerdere variabelen, waarbij beurtelings een (of meer) variabele(n) worden "vastgelegd", zoals

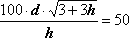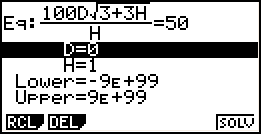
Ga als volgt te werk:

1. Kies uit het hoofdmenu EQUA
2. Kies F3 (Solver)
3. Typ achter Eq: de vergelijking in (m.b.v. ALPHA)
4. Geef de variabele die je vastlegt de gewenste waarde.(Hier : h=1)
5. Ga op de regel D= staan. Nu is d de variabele en wordt voor h de aangegeven waarde genomen.
6. Druk op EXE of op F6

De vergelijking is nu opgelost naar d.
Door voor D een waarde te kiezen en de cursor op de regel H= te zetten, kun je de vergelijking ook oplossen naar h.

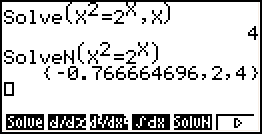
In het RUN- menu zijn Solve of SolvN op te roepen via OPTN F4 (CALC)

Een belangrijk verschil tussen beide is hiernaast te zien:

• Solve (komt overeen met de Solver in het EQUA menu geeft één oplossing.
• SolvN geeft meerdere oplossingen, vaak alle.

Bij gebruik van SolvN wordt gewaarschuwd dat er mogelijk nog andere oplossingen zijn. Dat is vaak wat overdreven, maar bij een vergelijking als cos x=0 zeer terecht.

Bij beide is het mogelijk het domein te beperken, bijv:

• Solve(X²=2^X,X,-1,0)
• SolvN(X²=2^X,X,-1,0)

In dit geval is het ook bij SolvN nodig om de gebruikte variabele (X) in te typen.!

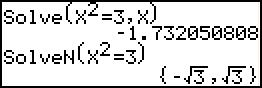
Een ander verschil tussen Solve en SolvN is dat de laatste soms exacte waarden geeft, vooral al ze te schrijven zijn als (een getal maal) een (tweedemachts) wortel, of een een getal maal π. (Helaas valt daar op dit moment niet veel meer over te zeggen).

In de meeste gevallen verdient SolvN de voorkeur boven Solve (of Solver).